Пропорции, перспектива и живописность в греческом искусстве
Глава «Пропорции, перспектива и живописность в греческом искусстве» раздела «Архитектура Древней Греции» из книги Огюста Шуази «История архитектуры» (Auguste Choisy, Histoire De L'Architecture, Paris, 1899). По изданию Всесоюзной академии архитектуры, Москва, 1935 г.
 |
|
| Рис. 232 | |
 |
 |
| Рис. 233 | Рис. 234 |
ПРОПОРЦИИ
При анализе ордеров нам непрестанно приходилось касаться идеи пропорций, т.е. определенных соотношений между различными частями, которые и придают каждому из этих основных ордеров его характерные признаки и накладывают на каждое архитектурное произведение отпечаток его эпохи. Мы исследуем сейчас закон, которым греки руководствовались при выборе пропорций.
Как и в архитектуре Египта и Месопотамии, у греков применялся главным образом модульный способ начертания. Он состоит в том, что все размеры целого связываются подчинением одной общей мере, взятой в самом здании. Эту основную единицу измерения называют модулем, все остальные размеры находятся к ней в простом кратном отношении.
Из памятников древней письменности мы знаем, что независимо от применяемого при постройке здания ордера – ионийского или дорийского – модуль всегда определялся радиусом колонны.
Долгое время считали, что речь шла о нижнем радиусе колонны. Безусловным сторонником такого толкования этой теории был Плиний, его, возможно, придерживался и Витрувий. Оно подтверждается несколькими памятниками римской эпохи, например колонной Траяна. Но оно не приложимо к памятникам Греции. Модульную систему уже начинали рассматривать как чистую теорию, не имевшую применения на практике, когда Орэс высказал мнение, что модулем служил средний радиус колонны, или, иначе говоря, полусумма крайних радиусов.
В первую очередь Орэс отметил, что отношение этого радиуса к различным частям композиции выражается числами, очень близкими к целым; во-вторых, этот радиус всегда выражается целым числом, если перевести на греческий, или вернее местный фут, который в Афинах был равен 0,308 м с подразделением на 16 дюймов, а в колоннах Великой Греции равнялся 0,296 м с подразделением на 12 дюймов.
Таким образом, точка отправления для дальнейших изысканий была найдена. Однако простота кратных отношений оправдывалась лишь с некоторой долей приближения. Исходя из положения, что в назначенном к точному исполнению проекте все размеры должны выражаться в целых числах, без дробей, Орэс с поразительной наглядностью объяснил все мнимые отклонения.
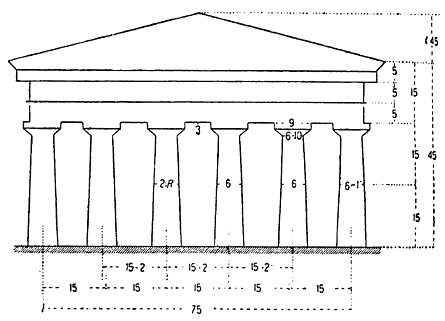
На примере Посейдонии (рисунок 232) мы лучше поймем его мысль.
Храм в Посейдонии. – Основным размером, определяемым величиной отведенной площади, является промежуток между осями двух крайних колонн: 75 италийских футов.
Этот промежуток должен быть подразделен на пять частей по числу интервалов между осями, что в середине определяет размер каждой из них в 15 футов. Но, как мы уже отмечали выше, в дорийском ордере крайние промежутки между осями обыкновенно бывали уже средних. Поэтому увеличивают расстояние между средними осями за счет крайних. Таким образом, вместо 15 футов средние интервалы имеют 15 футов и 2 дюйма, вследствие чего крайние интервалы сокращаются на 3 дюйма, т.е. равняются не 15 футам, а 14 футам и 9 дюймам.
Этот пример одновременно показывает нам и принцип и числовое выражение этих небольших отклонений.
Рассмотрим теперь одну за другой все части композиции.
Колонна. Ее высота равна двум промежуткам между осями, т.е. 30 футам. Средний ее диаметр (двойной модуль) соответствует одной пятой общей высоты, т.е. 6 футам. Следовательно, модуль равен 3 футам. Для придания, стволу конической формы диаметр базы увеличивают на 10 дюймов, а диаметр вершины настолько же уменьшают, что определяет размер диаметра базы в 6 футов и 10 дюймов, а диаметр вершины в 5 футов и 2 дюйма. Диаметр угловых колонн немного увеличивается по сравнению со средними: при диаметре средней колонны в 6 футов, диаметр угловой колонны будет равен 6 футам и 1 дюйму.
Верхние части ордера обычно имеют следующие размеры: архитрав и фриз одной высоты, по 5 футов каждый; такой же, вероятно, была и высота карниза в тех случаях, когда он бывал увенчан желобом. Таким образом, общая высота антаблемента равнялась 15 футам, или 5 модулям, или ширине промежутка между осями, или же, наконец, полувысоте колонны.
Перейдем теперь к исследованию капители (рисунок 233).
Ширина абаки равняется 9 футам, или 3 модулям. Высота капители, считая от основания эхина F, равна 3 футам (1 модуль) и делится на две равные части: эхин FC и абаку CB. Выступ эхина EF равен его высоте FC, а кривая его профиля вписывается в треугольник, основание которого относится к высоте, как 4:3 (пропорция египетского треугольника).
Что касается размеров деталей, то их можно определить по рисунку. Если принять R за средний радиус, r – за верхний радиус, а d – за разность двух радиусов, то все они явятся кратными числами в отношении R, r или d.
По этому примеру можно судить о характере всего метода: здесь одновременно видны и простые отношения размеров, которые дают то, что можно назвать теоретической пропорцией здания, и те числовые исправления, которые вызываются строительной практикой.
Еще один пример поможет нам окончательно понять особенности этого метода.
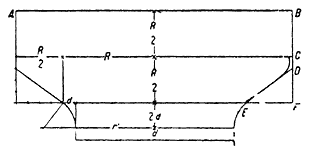
Арсенал в Пирее. – Все размеры этого здания известны нам из надписи, являющейся текстом договора на его постройку.
Восстанавливая фасад здания при помощи этих достоверных данных, мы находим между его различными частями в высшей степени простые отношения, которые мы постарались наглядно изобразить на рисунке 234. Основной величиной служит ширина AA' фасада, взятая поверх цоколя.
Высота фасада AB, взятая от цоколя до карниза, равна половине ширины AA'. Высота в середине CE равна двум третям AA'. Отверстия дверей равняются одной шестой ширины фасада, а высота их в полтора раза более ширины пролета. Венчающий двери карниз DD' расположен на половине высоты здания и по длине равняется половине ширины фасада.
Определим по масштабу все размеры в цифрах и перейдем к рассмотрению тех исправлений, которым они подверглись на практике.
Основная величина AA' (ширина фасада), определяемая, как и в Посейдонии, размерами отведенной под постройку площади, установлена в 55 футов. Исходя из этого размера, мы найдем все остальные, но так как они все будут выражены в дробных числах, то введем небольшую поправку, заключающуюся в округлении дробных чисел до целого.
Высота AB: в теории как половина 55 футов она должна бы равняться 27,5 футам. Эта цифра округляется до 27.
Высота CE: две трети 55 футов = 36,67 футам; округляется до 36.
Ширина двери: одна шестая 55 футов = 9,17 футам; округляется до 9.
Высота двери: три вторых 9 футов = 13,5 футам; округляется до 14.
Длина венчающего карниза DD'; половина 55 футов – так же, как и высота CE, округляется до 27.
Все греческие памятники, размеры которых могли быть точно установлены, следуют этим законам простых отношений, выражающих величины целыми цифрами, без дробей.
 |
 |
| Рис. 235 | Рис. 236 |
 |
|
| Рис. 237 | |
ПРОПОРЦИИ ОРДЕРОВ
Попытаемся теперь выразить в цифрах принятые в ордерах пропорции, причем постараемся выделить элементы постоянных пропорций, присущих ордерам, от изменений в их деталях, характерных для разных эпох.
Общий вид композиции. – Согласно замечанию Гитторфа, наиболее постоянное отношение существует между шириной и высотой фасада. При сравнении различных дорийских храмов с одинаковым количеством колонн, мы видим, что почти во всех случаях их колоннады вписываются в прямоугольник одной и той же формы. То же самое можно сказать и об ионийских храмах.
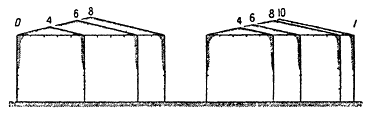
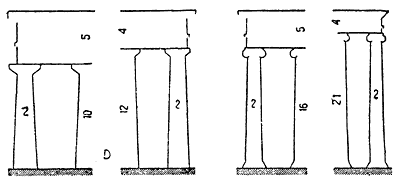
Рисунок 235, D показывает обычные пропорции дорийских фасадов в четыре, шесть и восемь колонн; рисунок 235, I – те же пропорции ионийских фасадов в четыре, шесть, восемь и десять колонн.
Из этих диаграмм видно, что в том и другом ордере, при наличии четырех колонн, фасад вписывается в прямоугольник, имеющий форму строгого квадрата. При наличии же шести и особенно восьми колонн прямоугольник в ионийском ордере значительно более удлиняется. Только два или три случая являются исключением из этого правила (Суний, Рамнунт, храм D в Селинунте).
Но всегда – и это самое существенное – отношение между шириной и высотой выражается целым числом.
Детали колоннад. – Если проанализировать детали колов над, то можно заметить, что в памятниках домакедонской эпохи некоторые отношения являются незыблемыми. Так, независимо от ордера высота архитрава равна высоте фриза. В качестве примера среди дорийских памятников можно назвать храм в Посейдонии (рисунок 232), храм Фесея, Парфенон, Пропилеи храм на мысе Сунии; среди ионийских памятников – храм на Плиссе, храм Ники Аптерос, Эрехфейон, храм в Милете, Мавзолей Галикарнасса.
В дорийских композициях высота капители делится на две равные части (эхин и абака) и соответствует ширине триглифа. Мы уже наблюдали равенства этих двух частей в Посейдонии (рисунок 233), в Метапонте, в храме Фесея, в Парфеноне.
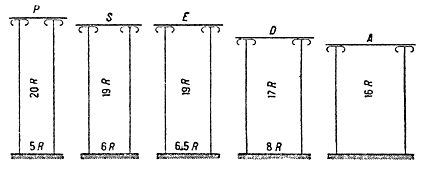
Остальные пропорции видоизменяются по эпохам. На рисунке 236 для сравнения указаны в круглых цифрах границы, в которых изменяются модульные отношения от архаической эпохи до македонского периода.
Даже при беглом сравнении элементов рисунка 236 можно проследить постепенное утончение колонны и соответствующее ему снижение высоты антаблемента. Если принять средний радиус за единицу, то высота колонны в дорийском ордере возрастает от десяти до двенадцати модулей, а в ионийском от шестнадцати до двадцати одного. Антаблемент же и в том и в другом случаях снижается с пяти до четырех модулей. В среднем же ионийский ордер, даже в самых робких своих пропорциях, представляется более легким, чем дорийский, в своих самых смелых.
Пропорции ордеров по Витрувию. – Витрувий передал нам методы определения пропорций, применявшихся в Александрийской школе. В основу их был положен следующий принцип.
Каков бы ни был ордер, Витрувий не допускает неизменного соотношения между толщиной колонн и размером интервалов между ними. Это отношение, главным образом определяющее характер силы или легкости произведения, он предоставляет выбору архитектора. Указанное отношение служит основанием для определения пропорций ствола: если колонны поставлены тесно, то их стволы будут стройными, в противном случае – приземистыми.
Что касается размеров капители, базы и антаблемента, то они непосредственно вытекают из величины радиуса или модуля; но так как и самый радиус устанавливается отношением между толщиной колонн и интервалами между ними, то можно сказать, что именно из этого характерного отношения вытекает весь ансамбль пропорций по Витрувию.
Уточним эти указания цифрами, взяв для примера ионийский ордер.
При толщине колонны, равной единице, Витрувий оставляет для интервалов на выбор следующие числа: 1 1/2, 2, 2 1/4, 3... Это – исходная точка, и, принимая ее за основу, Витрувий классифицирует колоннады как пикностиль, систиль и т. д.
Если отношение толщины колонн к интервалу между ними равно 11/2 или, другими словами, расстояние между осями колонн равняется пяти радиусам или модулям, высота колонны должна равняться двадцати модулям. Если расстояние между осями увеличивается до шести модулей R, то высота колонны снижается до девятнадцати R; при интервале в восемь R высота уменьшается до семнадцати R.
На рисунке 237 показаны существенные черты этого метода, который является не чем иным, как выражением в целых числах требования здравого смысла, чтобы колонны были тем более массивными, чем шире интервал между ними.
Когда вопрос касается гражданских зданий, Витрувий рекомендует пользоваться ордерами с более стройными пропорциями колонн и с более широкими интервалами между ними, но всегда подчиненными закону простых отношений; благодаря этому видоизменению, внутренняя площадь здания менее загромождается и вместе с тем избегает строгости стиля, которая уместна лишь в храмах.
МОДУЛЬ И МАСШТАБ
В греческой архитектуре только постройки архаической эпохи создают впечатление грандиозности массива. Это, по-видимому, зависит от самой громоздкости их пропорций.
Рассмотрим наиболее простой пример греческой конструкции, а именно антаблемент, не имеющий другой нагрузки, кроме собственной тяжести.
Анализ условий сопротивления показывает, что толщина этого антаблемента будет изменяться не в соответствии с увеличением пролета: так, при увеличении последнего в два раза она должна быть более чем удвоена. Другими словами, антаблемент крупных размеров оказывается более массивным, чем антаблемент над малыми пролетами.
Зато массивный антаблемент создает со своей стороны впечатление крупного сооружения, как например в храме Посейдонии, где преувеличенная массивность обусловливает иллюзию грандиозности здания.
Мы не будем утверждать, что такое преувеличение было преднамеренным, но создаваемое им впечатление является, по-видимому, присущим только архаическому периоду. Начиная с V в., греки обнаруживают стремление к оформлению ордеров, исходя из канона пропорций, не связанных с масштабом; мало-помалу они настолько поддаются влиянию этого метода, что поступаются ради установленных пропорций даже требованиями материальных удобств.
Нам представляется, например, что некоторые элементы архитектурного целого должны были бы сохранять, независимо от размеров здания, приблизительно одинаковый размер. Рассматривая проблему с чисто утилитарной точки зрения, казалось бы, что высота двери должна определяться исключительно высотой человеческого роста, а высота ступеней – сообразовываться с шагом человека, которому предстоит подниматься по ним.
Однако, если греки вообще руководствуются этими соображениями, то никак не далее архаического периода искусства, и очень скоро окончательно упускают их из вида. Они подчиняют постепенно размеры всех элементов здания модульному канону и увеличивают или уменьшают их в зависимости от увеличения или уменьшения модуля. Так, например, удваивая обмеры фасада, они одновременно удваивают высоту дверей и высоту ступеней. Исчезает всякая связь между назначением конструктивных частей и их размером; не остается ничего, что могло бы служить масштабом здания.
Архитекторы средневековья сумели согласовать пропорции, устанавливающие архитектурный ритм, с указаниями спасительного масштаба, дающего возможность определять размеры. Мы увидим, что установленный абсолютный размер определял разработку пропорций в частной архитектуре Рима.
Весьма возможно, что гражданская архитектура греков, если бы она дошла до нас в большей сохранности, также дала бы нам пример сооружений, где масштаб играл известную роль. Но в архитектуре храмов греки признают исключительно ритм. Их архитектурные произведения, по крайней мере относящиеся к последнему периоду, представляют собой как бы отвлеченную идею. Не связанные ни с чем, поддающимся измерению, они не вызывают никаких представлений об абсолютных величинах, а только чувство соотношений и впечатление гармонии.
КОРРЕКТИРОВАНИЕ ОПТИЧЕСКОГО ОБМАНА
Эффекты расстояния. – Вышеописанные методы модульного построения и графических приемов оценивались отрицательно за то, что они создавали мнимую гармонию, не выдерживающую изменений перспективы.
Однако воображение зрителя восстанавливает фактические размеры и схватывает приблизительно верные соотношения. Тем не менее существует известная доля оптических обманов, с которыми приходится считаться. Проблема эта сложна, и она усиленно привлекала пытливую мысль греков.
В диалоге Платона «Софист» сказано, что у греков было в обычае увеличивать высоту частей, рассматриваемых снизу и уменьшенных поэтому перспективой.
Витрувий уточняет это указание общего характера:
Деформация увеличивается для зрителя, находящегося у подножия здания, пропорционально размерам последнего: стволы колонн утончаются, антаблемент кажется более узким, чем в действительности, а косяки дверей – преувеличенно наклонными.
Этот оптический обман корректируется нарочитым увеличением тех элементов, которые уменьшает перспектива, и сокращением тех, которые она увеличивает: умеряют утончение колонн, сдерживают наклон дверных косяков и слегка утолщают части антаблемента.
Таково правило, сформулированное Витрувием.
Следуя данной тенденции и совершенно не стремясь выражать материальные размеры здания, подчинив их соотношения масштабу, греки теряют, так сказать, всякий след масштабности и приводят все здания, независимо от их размера, к единому облику.
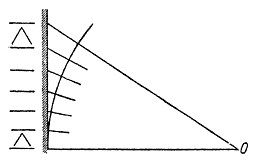
Мы имеем возможность уяснить себе по весьма бесхитростному приему в храме в Приене сущность описываемого метода корректирования оптического обмана. В надписи, выгравированной на одной из ант, высота букв изменяется по строчкам (рисунок 239). Для зрителя, находящегося в точке O, отсекаемая высота угла каждой строки выравнивается, и получается впечатление букв одинаковой величины.
 |
| Рис. 239 |
Исходя из положения, что глаз воспринимает только соотношения углов, Паннеторн считает метод, примененный для надписи в Приене, характерным вообще для методов греческого искусства. Разбирая, между прочим, и Парфенон, он отмечает некоторые точки, откуда архитектурные массивы дают под известным углом зрения простые соотношения. По его мнению, архитектор прежде всего доискивался именно этих соотношений углов.
Соглашаясь безоговорочно с данной теорией, следовало бы прежде всего принять закон углов, который сам автор установил только приблизительно, и предположить далее, что здание было задумано с расчетом на одну исключительную точку зрения. Глаз может менять положение, однако углы зрения сравнительно мало изменяются даже при значительных перемещениях. Однако теория Паннеторна все же выражает как будто, по существу, верную мысль; ее нельзя выразить формулой, но она указывает на определенную тенденцию.
Прием корректирования оптических обманов свойственен не одной только архитектуре, мы встречаемся с ним и в скульптуре. Один из византийских авторов сообщает нам о том неблагоприятном впечатлении, которое произвели на него фигуру предназначенные для фронтона Парфенона, снятые с их надлежащего места: они оказались преднамеренно искаженными с учетом действия перспективы.
Статуи, украшающие фронтон храма Олимпии, кажутся неуклюжими, если на них смотреть прямо, но приобретают неожиданную красоту и изящество, как только мы взглянем на них снизу вверх. Как Фидий в Парфеноне, так и Пеоний в Олимпии принимали в расчет предполагаемые точки зрения; и все статуи великой эпохи греческого искусства создавались именно для того места, которое они должны были занимать.
Если греки старались в ряде случаев корректировать оптический обман, нарушающий гармонию, то были случаи, когда они, наоборот, намеренно его вызывали.
В портиках с двойным рядом колонн колонны второго ряда делались обычно более тонкими, чем стоящие впереди. Таким образом, они казались одинаковых размеров с передними, но более отдаленными от них, чем это было на самом деле; этим создавалось впечатление большей глубины. Мы с трудом находим несколько случаев, и то только среди зданий архаической эпохи, как например храм S в Селинунте или древний храм Сиракуз, где колонны двойной колоннады портика были бы одинаковых размеров. Это различие отмечается во всех без исключения портиках V в. Колонны Парфенона отличаются друг от друг как высотой, так и диаметром.
 |
 |
| Рис. 240 | Рис. 241 |
 |
 |
| Рис. 242 | Рис. 243 |
 |
|
| Рис. 244 | |
ЭФФЕКТ ИЗЛУЧЕНИЯ И КОНТРАСТОВ. ОПТИЧЕСКИЙ ОБМАН ГОРИЗОНТАЛЬНЫХ И ВЕРТИКАЛЬНЫХ ЛИНИЙ
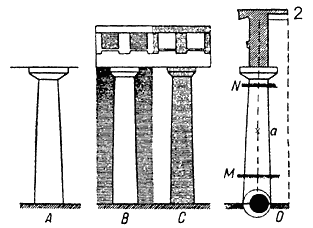
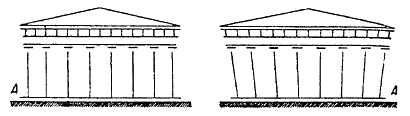
Энтазис колонн. – Мы читаем в одном греческом трактате по оптике, что правильный цилиндр кажется сжатым посередине. Дамиан Ларийский мог бы с тем же успехом употребить вместо «цилиндра» слово «колонна». Греки стремятся исправить это кажущееся сжатие (рисунок 240, A), придавая стволу колонны некоторую выпуклость. Таково происхождение той кривой, которая уже была описана выше под названием энтазиса.
Утолщение боковых колонн. – Греки не только исправляли ввиду зрительного обмана профиль колонны, но принимали также в расчет и влияние излучения, искажающего впечатление их толщины (рисунок 240, B и C).
Угловая колонна храма, выделяющаяся на фоне неба, кажется, по выражению Витрувия, «поглощенной окружающим светом». В целях корректирования этого явления такие колонны утолщают, что мы видим на примере храма в Посейдонии.
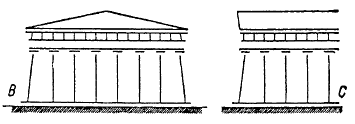
Наклон колонн. – Колонны имеют не только правильную линию профилей, но и не строго вертикальную ось X. Витрувий предписывает придавать оси X колонн легкий наклон, направленный внутрь здания, и правильность его указания подтверждена примерами архитектурных памятников.
Наклон оси колонны осуществляется следующим образом. Верхняя поверхность M первого барабана колонны обрабатывается перпендикулярно оси X; ствол колонны соединяют с капителью при помощи верхнего отрезка N с непараллельными плоскостями, и колонна возводится, таким образом, так же легко, как если бы она была совершенно прямой.
Наклон осей с направлением внутрь здания может быть оправдан соображениями относительной устойчивости и, так или иначе, настолько соответствует действительному требованию, что в зданиях, где он отсутствует, оси колонн кажутся расходящимися веером.
Все современные здания с вертикально поставленными колоннами производят именно такое впечатление: и парижский Пантеон, и Палата депутатов кажутся расширяющимися кверху.
Описанное явление изображено в утрированном виде на рисунке 241, а на рисунке 242 показывается способ его исправления, применявшийся греками. Колонны и даже архитрав имеют некоторый уклон, противоположный тому, который сообщается оптическим обманом.
Наклон фронтонов. – Современные здания создают еще и другое неправильное впечатление: их фронтон не кажется вертикальным.
Это явление было знакомо Витрувию: «Если фронтон сделан вертикальным, то будет казаться, что он отходит назад».
Витрувий советует поэтому делать фронтон несколько нависающим вперед (рисунок 242, C). Плиты фронтона Парфенона образуют навес, создающий очень благоприятное впечатление однако их современное положение может быть обусловлено изменением формы и не является следствием системы первоначальной укладки.
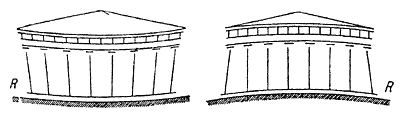
Замена горизонтальных линий кривыми. – Приведем еще один пример оптического обмана, наблюдаемого на фасадах современных зданий (рисунок 243, R): одновременно с расхождением вертикальных линий наблюдается как бы прогиб горизонтальных линий антаблемента, и создается впечатление, что колоннада прогибается в центре под чрезмерной тяжестью фронтона.
Это явление не прошло для греков незамеченным, и они старались исправить его, фактически выгибая линии по кривой в направлении, противоположном кажущемуся прогибу. Таким образом, мы получаем для Парфенона, несколько утрируя как изгиб крыши, так и наклон колонн, – положение, данное на рисунке 243, R.
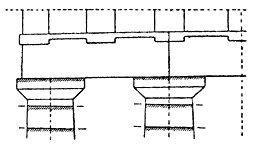
На рисунке 244 показано в преувеличенном виде изменение формы капители, объясняемое кривизной линии архитрава.
Выпуклость плит пола. – Совершенно ровный пол кажется вдавленным посредине; во избежание этого полу Парфенона придана легкая выпуклость.
Время и происхождение методов исправления оптических обманов. – Эти остроумные методы, состоявшие в противопоставлении кажущемуся искривлению линий и поверхностей искривлений в обратном направлении, отмечаются у греков не ранее середины V в., но их принцип был известен уже египтянам.
Парфенон имеет прямые линии в горизонтальном плане и кривые в вертикальном; в храме же Мединет-Абу линии искривлены в горизонтальном плане, но сохранены прямыми в вертикальном. Иными словами, кривизна наблюдается у египтян в горизонтальной плоскости, а у греков – в вертикальной. В том и другое случаях получается один и тот же результат: кривые Парфенона и Мединет-Абу являются только двумя различными способами для достижения одного и того же оптического впечатления.
Все указанные искривления настолько незначительны, что ускользнули даже от внимания таких наблюдателей, как Стюарт.
Стрела прогиба, измеренная Пенрозом, равнялась 0,065 м на 100 футов, или, круглым счетом, но 30 м по главному фасаду и 0,123 м на 70 м бокового фасада.
Указанную кривизну линий нельзя отнести за счет осадки здания: грунт, на котором построен Парфенон, представляет собой скалу, а его основание сложено насухо из каменных глыб.
Кроме того, Витрувий говорит о методе изгибов как о приеме, сохранившемся до римской эпохи, причем объясняет их уже приведенными соображениями, а именно исправлением оптического обмана, не поддающегося более или менее точному объяснению, но фактически не подлежащего никакому сомнению.
Теория Витрувия была бы убедительной, если бы незначительная стрела прогиба создавала впечатление прямой линии. На самом же деле мы имеем вполне ощутительный изгиб.
Означает ли это неудачу? Ни в какой степени. Это необычайное расположение линий создает сознательное или бессознательное впечатление чего-то оригинального и нового. Непредупрежденный зритель чувствует эту необычность, но потом разбирается в тонком, чарующем его замысле. Контуры здания принимают благодаря этому изысканному расположению, изящество, мимо которого нельзя пройти равнодушно; здание теряет вульгарный вид сооружений с прямыми линиями и приобретает совершенно новый и неожиданный характер, не поддающийся, быть может, анализу, но действующий на нас даже тогда, когда мы не знаем его истиной причины и смысла.



Добавить комментарий